BJT

---

GATE PRACTICE PROBLEM ON BJT - 1

In this circuit, the 10nF capacitor is initially charged to 5V. The NPN transistor is driven with a 40 micro-sec period rectangular wave going from 0 to 3.7 V and an ON duration of Ton. Determine Ton so that the transistors never leave the active region even after an arbitrarily long time. NPN and PNP transistors are active with Vbe= 0.7 V and Veb= 0.7V respectively.

---

Solution: This is our 2nd problem on "GATE Revision". For the first problem check index.

The initial voltage across the capacitor is 5 V. From the given data we can conclude that pnp BJT is always on. On the other hand, npn transistor is on when the voltage applied at the base is 3.7 V. So \(V_{Ep}= 7.3+0.7 = 8 V\) and \(V_{En}= 3.7-0.7 = 3 V\).

---

Current through 5K resistance is \(I_{5K} = 2/5k = 0.4 mA \).

Current through 3K resistance is \(I_{3K} = 3/3k = 1 mA \).

At \( t=0 sec \) , \(V_{Bn}= 3.7 V\) . The equivalent circuit looks like

As the circuit suggests capacitor discharges with a constant current of 0.6 mA. We can formulate the capacitor voltage w.r.t. time as below

\[V_{C}=V_{C0} - \frac{I}{C}\times t\]

At \(t=T_{on}\), \[V_{C}=5 - \frac{0.6\times 10^{-3}}{10\times 10^{-9}}\times T_{on}\]

To ensure npn transistor, not going to saturation ever, Condition is \(V_{CB}>0\)

\[=>V_{CB}=5 - \frac{0.6\times 10^{-3}}{10\times 10^{-9}}\times T_{on}- 3.7>0\]

\[=>T_{on}<21.66  \mu sec\]

---

Now to check for pnp BJT for every condition. when square wave input is 0V, the npn transistor is off. Capacitor gets charged by pnp transistor. The value of the charging current is 0.4 mA.

\[V_{C}=3.7 + \frac{0.4 \times 10^{-3}}{10\times 10^{-9}}\times (T-T_{on})\]

\[V_{CBpnp}<0\]

\[=>V_{CB}=3.7 + \frac{0.4 \times 10^{-3}}{10\times 10^{-9}}\times (T-T_{on})-7.3<0\]

\[=>40-T_{on}<90\]

Which is always true for \(T_{on}=21.66 \mu sec \)

But the above answer is not true for all the cycles. The assumption, here made that the initial voltage is 5V. That value may change after each cycle. So is that a problem? Remember that, we have to ensure "transistors never leave the active region even after an arbitrarily long time".

---

There are two phases -----------
Phase-I: capacitor is discharged by a constant current of 0.6 mA. (both transistors are on)
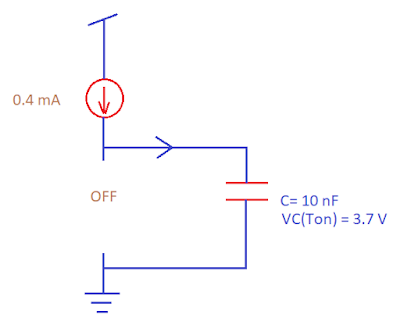
Phase-II: The capacitor is charged by a constant current of 0.4 mA.(only pnp is on)
Consider, 
Phase-I: Voltage across the capacitor is decreased by Vx (from the time t= 0 to t=Ton)
Phase-II: Voltage across the capacitor is increased by Vy (from the time t=Ton to t=T )

First cycle 

t=0,  Vc(0) = 5 ; 
t=Ton,  Vc(Ton) = 5-x ;
t=T,  Vc(T) = 5-x+y ;

Second Cycle 

t=T,  Vc(T) = 5-x+y; 

t=T+Ton,  Vc(T+Ton) = 5-2x+y 

t=2T,  Vc(2T) = 5-2x+2y

If you observe, at the end of each cycle  Capacitor voltage is increased by y-x

if y > x - Vc will rise with each cycle pass. When Vc > 7.3 V, pnp goes into saturation. 

if x > y - Vc will fall with each cycle pass. When Vc < 3.7 V, npn goes into saturation. 

the option left is  x=y.

\[\frac{I_{dischage}}{C}\times T_{on} = \frac{I_{charge}}{C}\times (T-T_{on})\]

\[=>I_{dischage}\times T_{on} = I_{charge}\times (T-T_{on})\]

\[=>(I_{dischage}+I_{dischage}) \times T_{on} = I_{chage}\times T\]

\[=>T_{on} = T\times \frac{I_{charge}}{(I_{dischage}+I_{dischage})}\]

\[=>T_{on} = 40\times \frac{0.4 \, mA}{(0.4 \, mA + 0.6\, mA)} \: \mu sec\]

\[=>T_{on} = 16 \: \mu sec\]

---

If you have any doubt on this Diode Logic problem, let me know in the comment section. GATE and campus placement related tutorial click here.

For Problems on network Theory GATE and campus placement click here.

If you have any doubt, let me know in the comment section. For other tutorials check INDEX. For further updates follow my blog (rlcanalog.blogspot.com). The blog is specially made for GATE and VLSI aspirants (GATE Electronics( GATE & VLSI)).