TEXAS INSTRUMENTS INTERVIEW QUESTIONS PART-2

In the last post, I discussed my interview experience. In this post, I shall take forward that discussion.

The interviewers asked some basic questions on network theory and op-amp which mostly asked to a 3rd year BTech. student, applying for the internship.
Let's have an insightful discussion.

Q4)

Solution:

This is a very basic question. It's asked to test your understanding of network theory. Immediately one should identify the fact that current through the 1K resistor is zero. Why so? Let me help you...

Here the circuit is partitioned into two parts. If circuit A provides a Current to circuit B through the 1K bridge resistor, there must be a path to accommodate the current from circuit B to A also. Due to the unavailability of a path to return the current, current through the bridge resistor is zero. Now the rest is easy.

So \[V{x}= 0+2+0-3=-1V\]

Trick: When you try to find out the potential of any node from another node, the voltage will be added if you traverse from '-' to '+'.

Q5)

Solution:

This is a special circuit. For a particular condition, it acts as a differential amplifier with an infinite common-mode rejection ratio.

At first, let me share the way I solved in the interview. Later on, I will give a complete overview of the circuit.

For an ideal op-amp, both the input nodes are virtually shorted. Due to infinite input resistance, op-amp allows no current at the input.

Consider

\[V^{+}=V^{-}=V_{A}\]

Assume the current direction through the resistor connected in between the positive terminal and the ground is downward. The direction of current through other resistor are shown accordingly. The voltage drop across the resistors is the same for all the resistors.

\[V^{-}=V^{+}+V_{A}+1+V_{A}\]

\[=>V_{A}=-0.5=V^{-}\]

now,

\[=>V{out}=V^{-}+V_{A}=-0.5-0.5=-1\]

After that interviewers asked whether my assumption for the direction of the current is correct or not? In reply, I said no.

Now come to the specialty of the circuit.
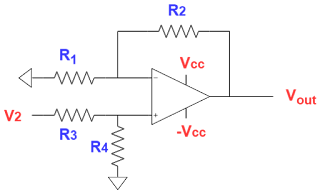
Take the below circuit

If we apply the superposition theorem to solve this circuit. First V2=0.

\(V^{+}=0=V^{-}\)

Applying inverting amplier gain formula

\[V_{out,V1}=-\frac{R_{2}}{R_{1}} \times V_{1}\]

Consider V1=0

Applying non-inverting gain formula

\[ V_{out,V2}=\frac{R_{4}}{R_{3}+R_{4}}\times (1+ \frac{R_{2}}{R_{1}}) \times V_{2}\]

Consider the condition R2/R1 = R4/R3

\[V_{out,V2}=\frac{R_{2}}{R_{1}} \times V_{2}\]

For the above condition

\[ V_{out}=V_{out,V1}+V_{out,V2}=\frac{R_{2}}{R_{1}} \times (V_{2}-V_{1})\]

In our case (V2-V1)= -1V so, Vout = -1V

Previous Page Index

If you have any doubt, let me know in the comment section. For other tutorials check INDEX. For further updates follow my blog (rlcanalog.blogspot.com). The blog is specially made for GATE and VLSI aspirants (ANALOG INTUITION ( GATE & VLSI)).

Important question on 'GATE EC'

For any gate aspirant, the most challenging part of the preparation is revision. There are 10 subjects for EC. To deal with all those subjects you need the right strategy. During my preparation days, I followed a technique which I named "Hammering of your brain".

How does this "hammering of your brain" technique work? Let me break it to you...........

First, clear the basics of all the 10 subjects. Do practice previous year gate questions asked in a subject (topic-wise) while preparing for any particular subject. Now, suppose after one month or so you want to revise a particular subject. What do you do?

You will again start reading those subjects from notes or have a look at the important parts, right? I say don't do that! In your brain, that is more volatile in nature. Eventually, after few weeks most of it will go by far in space. So what I suggest, pick a question randomly from any particular topic you want and start solving. Do that without giving a look at its background theory again (which you have already covered many times while reading that topic the first time). If you can solve that problem, that's good. If not, go check for the theory or background concept (only that part especially, nothing more!). That way your brain gets used to the unusual situation. Your brain will automatically make a permanent space for that particular topic. That's a hammer I say, stretch your permanent storage of brain every day little by little.

Now without making it boring ( what was that before! LOL) let's come to today's topic. I will take a problem on network theory which will be useful for your revision.

\[V_{in}= 50 + 5\sin t, \; \; R= 50 K\Omega \; \; V_{Oavg}=7.5V\]

\[V_{in}= 100 + 10\sin t, \; \; R= 100 K\Omega \; \; V_{Oavg}=20V\]

then find out \(V_{Oavg}\) if \(V_{in}= 100 + 10\sin t, \; \; R= 150 K\Omega \; \; V_{Oavg}=?\) (capacitor value is constant and high)

Solution:

Now assume Capacitor is short-circuited in any finite signal frequency. Let's redraw the circuit.

So we don't need to worry about ac signal at all . That's relaxing! Also important thing is we don't need to find out the Zth (Thevenin Impdanace) rather we shall find Rth (Thevenin's resistance). Let's make some equation and find out that.

Due to the homogeneity property of a Linear system we can write \(V_{th}=K \times V_{in}\).

Now just redraw the whole thing for the last time

\[V_{O,avg}= K\times V_{in} \times \frac{R}{R+R_{th}}\]

Now we can get two equation

\[7.5= K\times 50 \times \frac{50}{50+R_{th}} \; \; \; (1)\]

\[20= K\times 100 \times \frac{100}{100+R_{th}} \; \; \; (2)\]

Solving above two equation you get

\[K=0.3 , \; R_{th}=50\]

Now put those value find the answer

\[0.3\times 150 \times \frac{150}{150+R_{th}} = 33.75\]

Hope you have enjoyed the question. Stay connected for more updates.

Analog Intuition (GATE & VLSI)

Recent